Keras kitabxanasıyla Süni Neyron Şəbəkəsi yaradarkən xəta/itki funksiyalarının seçilməsi
Mündəricat
- Empirik/təcrübi hesablamaya giriş, Nümunə məsələ (xətti reqressiya)
- Xəta funskiyaları (cost functions)
- Mühüm qeydlər
- İtki funskiyası seçimində addımlar ardıcıllığı
- Nəticə
- Ədəbiyyat
Empirik/təcrübi hesablamaya giriş, Nümunə məsələ (xətti reqressiya)
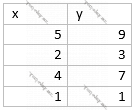
Təsəvvür edin, yuxarıdakı cədvəldə olduğu kimi müşahidələr verilib. Biz isə ixtiyari bir x qiyməti verildikdə y qiymətlərinə yaxın qiymətlər hesablayacaq bir f(x) funksiyası tapmalıyıq. Bu (x, y) nöqtələri haradasa bir xətt üzərində düzülüb. Deməli, f(x) funksiyası hansısa xətti funksiya olmalıdır.
Əgər f(x) = p0+p1x desək, bizə sadəcə verilmiş (x, y) cütləri əsasında f(x) funksiyasının qiymətlərinin x-lə necə əlaqələndiyini göstərən p0 və p1 əmsallarını tapmaq qalır. Hansı ki, bəzi yanaşmalar var ki, bu işdə bizə kömək edir. Belə ki, bizim modelimizin tapacağı f(x) qiymətləri ilə bu x-lara uyğun real y qiymətlərinin fərqini minimal edəcək p0 və p1 tapa bilsək, özümüzü verilmiş x qiyməti üçün real y qiymətinə maksimal yaxın qiymətlər hesablayan f(x) funksiyasını tapmış saya bilərik. Və:
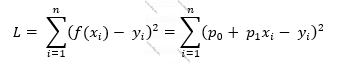
Burada n f(x) funksiyasının p0 və p1 əmsallarını əsasında hesablayacağımız müşahidələrin – (x, y) cütlərinin sayı, (xi, yi) i-ci müşahidənin qiymətləri, ∑ cəmləmə operatoru, f(x) isə modelimizin xi-yə uyğun yi-yə yaxın tapacağı (xi-yə görə proqnozlaşdırdığı) ədəddir.
Deməli, verilmiş (x, y) cütlərindən f(x)-ı tapmaq üçün L(p0, p1) funksiyasını minimallaşdırmalıyıq. (1≤i≤n olduqda (xi, yi) cütləri verilib.)
Bir dəyişənli funksiyaya minimum qiyməti verən parametr qiymətlərini taparkən necə ki, həmin funksiyanın həmin parametrə görə törəməsini tapıb 0-a bərabərləşdirib alınan tənliyi həll eləyirdik, eləcə də, 2 dəyişəndən (burada p0, p1-dən) asılı L(p0, p1) funksiyasını minimal edəcək p0, p1 qiymətlərini tapmaq üçün L(p0, p1) funksiyasının p0 və p1-ə görə xüsusi törəmələrini tapdıqda alınan iki ifadəni ayrı-ayrı 0-a bərabərləşdirdikdə alınan tənliklər sistemini həll etmək lazımdır.
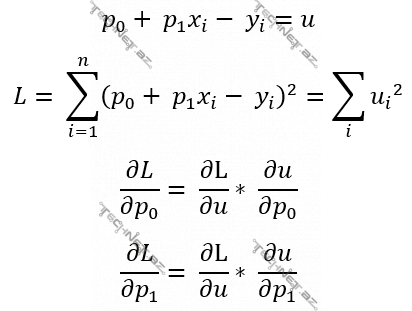
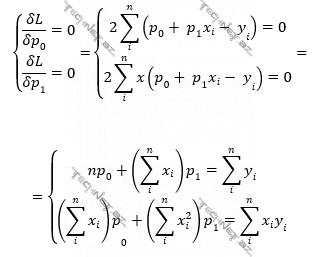
Hansı ki, bu yuxarıdakı son tənliklər sistemini matrislər və vektorlarla belə yazmaq olar:
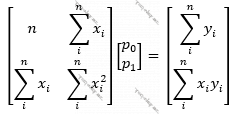
Və əgər:

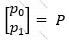
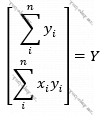
Onda
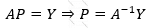
Olur. Nəzərə alsaq ki, bizim əsl məqsədimiz P = [p0, p1]-i tapmaq idi, Burada A-1 – A matrisinin tərsini tapıb Y vektoruna vurmaq kifayət olacaqdır.
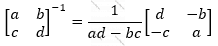
… kimi tapıldığına görə:

Deməli:

… olur. Deməli, p0, p1 parametrlərini verilmiş (x, y) cütləri ilə tapmaq olar:
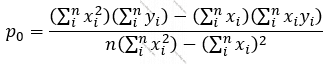
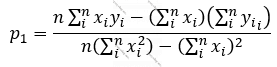
Ancaq bütün bu yuxarıda yazılanları verilmiş X, Y vektorlarına (array-lərinə) görə yerinə yetirən hazır funksiyalar var. Və işin riyazi dərinliyinə düşməyə sırf ona görə ehtiyac var idi ki, maşın öyrətməsi alqoritmlərinin əsasında dayanan əsas məsələni anlayaq. Belə ki, bizim yuxarıdakı xətti reqressiya məsələsini həll edərkən etdiyimiz kimi süni neyron şəbəkələri də hansısa funksiyanın müəyyən parametrlərə görə optimallaşdırılması (minimallaşdırılması-maksimallaşdırılması) nəticəsində yaranır.
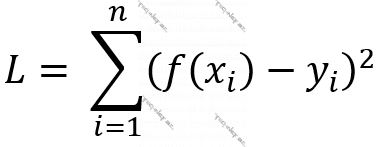
Kimi bir xəta funksiyasını bir Süni Neyron Şəbəkəsində də istifadə edə bilirik. Və bu yuxarıdakı o funksiyalardan sadəcə biridir. İndi gəlin onlara ayrı-ayrılıqda baxıb, hər funksiyanın nə vaxt, niyə istifadə olunduğunu deyək.
Qeyd: Mən burada yalnız python diliylə işləyən tensorflow platformasında fəaliyyət göstərə bilən keras kitabxanasındakı istifadə oluna bilən xəta funksiyalarından (cost functions) bəhs açacağam. Və bilməyənlər üçün deyim, keras python diliylə süni neyron şəbəkəsini asanlıqla qurmağa icazə verən kitabxanadır. Bir qeyd olunmalı məqam daha var ki, əslində konsepsiyanı başa düşmək asan olsun deyə burada xəta funskiyası (cost function) terminini istifadə edirəm. Əslində keras kitabxanasında biz itki funksiyasını (loss function) istifadə edirik, ancaq xəta funksiyası (cost function) da bütün müşahidələrə uyğun itki funksiyaları qiymətlərinin cəmidir. “Düstur: xəta funskiyası” açıqlamalı şəkildəki cəm işarəsinə nəzər salsanız, nəyi nəzərdə tutduğumu başa düşəcəksiniz. Əgər yenə də başa düşməsəniz, qeyd edim ki, məqalənin sonunda bu məsələyə bir daha qayıdacağam.
Xəta funksiyaları (cost functions)
Funksiya 1. Orta Kvadratik Xəta (Mean Squared Error/Quadratic Loss, MSE) [1]
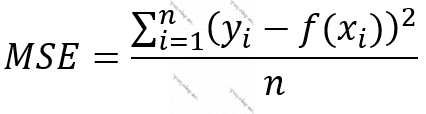
Bu funksiyada bir (x, y) müşahidəsi/nöqtəsi ümumi xətaya çox təsir edir. Məsələn, y3-f(x3)=5 dirsə, (y3-f(x3))2=25 eləyir. Modelin hər müşahidədə elədiyi xəta ümumi xəta ədədinə kvadrata yüksəldilərək əlavə olunur. Bu isə o deməkdir ki, model “outlier” dediyimiz kənaraçıxmaları da ciddi qəbul edəcək. Aşağıda (4, 1) nöqtəsi olmayan və olan qrafiklər arasındakı fərqə baxın.
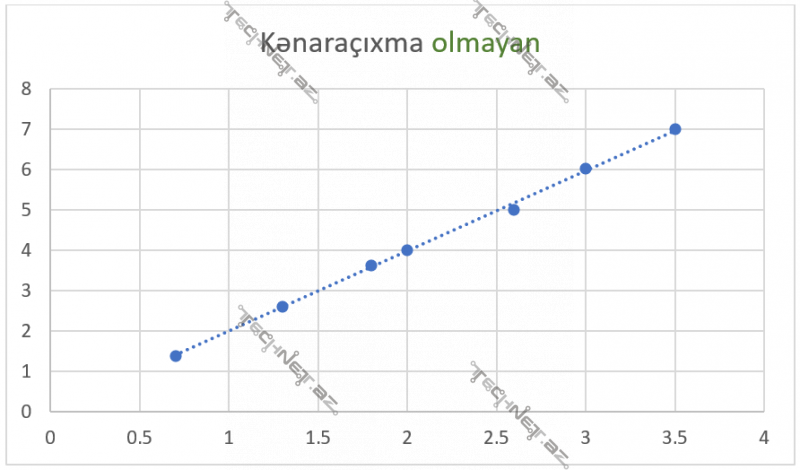
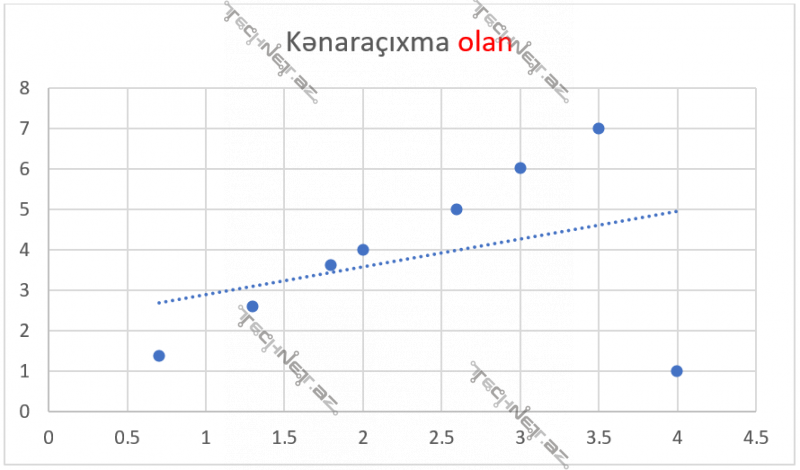
Ancaq bu funksiyanın (MSE) kənaraçıxmaları çox güclü nəzərə alması ona görədir ki, bu funksiya öyrədiləcək məlumatı çox yaxşı öyrədir.
Unutmayın ki, maşın öyrətməsində məlumatın çoxluğuyla birlikdə məlumatın doğruluğu, dəqiqliyi də mühümdür. Və əgər modelinizi öyrətmək istədiyiniz məlumatların doğruluğuna inanırsınızsa, bu funksiya modelinizi həmin doğru məlumatlara əla öyrədəcək.
Funksiya 2. Orta Mütləq Xəta (Mean Absolute Error, MAE) [1]
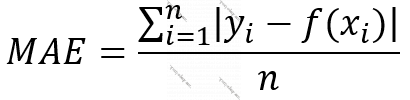
Hər müşahidəyə uyğun xətanı kvadrata yüksəldərək əlavə edən yuxarıdakı funksiyadan (MSE-dən) sonra yəqin ki, bu metodun niyə istifadə olunduğu aşkardır. Əgər məlumatları model qismən az öyrənsin istəyiriksə bu metodu işlədirik. Bu metodda kvadrat-filan olmadığından, funksiyanın qrafiki xəttidir. Bu da o deməkdir ki, hər müşahidənin xətasının ümumi xəta ədədinə təsiri xətti asılılıqdır. MSE-dəki kimi kvadratik deyil.
Funksiya 3. Orta Mütləq Faiz Xətası (Mean Absolute Persentage Error, MAPE) [2]
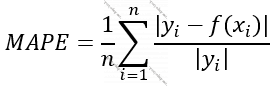
Böyük ədədlərlə işləmək üçün lazımdır. Məsələn, öyrədiləcək müşahidələrin sayı 50000-dirsə, biri var, milyarda çatan 50000 ədədin cəmini hesablamaq – ki, bir çox proqramlaşdırma dilində bu, xüsusi kitabxanalar olmadan mümkün deyil, bu da çox vaxt aparır – biri də var hesablamaları həmin milyardlıq ədədləri 0 və 1 arası ədədlərə – faiz ədədlərinə çevirərək aparaq.
Problemləri:
- Öyrədiləcək müşahidələrdən hansısa nəticə kimi 0-a sahibdirsə (müşahidənin real nəticəsi 0-dırsa), 0-a bölmək mümkün olmadığından həmin müşahidəni MAPE hesablamasına daxil etmək olmur. Bunun üstəsindən gəlmək üçün hesablamada istifadə olunan həmin ədədə çox kiçik bir ədəd əlavə etmək lazımdır ki, hesablamada 0 olmasın, ancaq “sıfır kimi” bir kiçik ədəd olsun.
- yi-nin f(xi)-dən böyük olması f(xi)-nin yi-dən böyük olmasından çox fərqlidir. Məsələn, real nəticə 100, proqnozlaşdırılmış 70-dirsə, axtardığımız ədəd 0.3 ((100-70)/100=0.3); real nəticə 40, proqnozlaşdırılmış 70 olarsa, axtardığımız ədəd 0.75 ((70-30)/40) olur. Halbuki, real nəticə ilə proqnozlaşdırma arasındakı fərq hər iki halda eyni, 30-dur. [18]
Funksiya 4. Orta Kvadratik Loqarifmik Xəta (Mean Squared Logarithmic Error, MSLE)
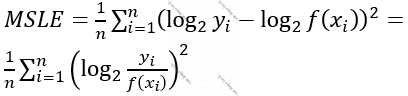
- Real nəticələr ilə modelin proqrnozlaşdığı nəticələrin müqayisəsini fərq yox, qismət əsasında aparır. Bu da imkan verir ki, (y=30, f(X)=20) ilə (y=30000, f(X)=20000)-ə eyni davranılsın.
- Ancaq MSLE də MAPE kimi real nəticənin modelin nəticəsindən çox olması ilə modelin nəticəsinin realdan çox olması arasına fərq qoyur.
- yi və f(xi) qiymətlərindən hər hansı biri 0 qiymət alsa loqifmləri hesablamaq mümkün olmur deyə, bu qiymətlərə çox kiçik bir ədəd əlavə olunur. Hansı ki, bu kiçik ədəd xəta funksiyasının aldığı qiymətə elə bir təsir etmir, ancaq loqarifmi sıfır olmağa da qoymur. [3] Xatırlayırsınızsa, bu üsulu MAPE üçün də istifadə etmək mümkün idi.
- Loqirfm mənfi qiyməti götürə bilmədiyindən modelin ən az son layı/səviyyəsinin (layer-i) siqmoid kimi aktivasiya funksiyasından istifadə olunaraq normallaşdırılması məqsədəuyğundur. Çünki siqmoid 0-la 1 arasında qiymətlər verir.
Funksiya 5. Huber funksiyası/Hamar Orta Mütləq Xəta (Huber, Smooth Mean Absolute Error)
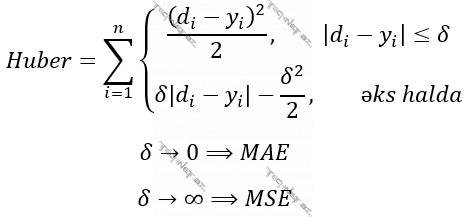
- Huber funksiyası fərqli X aralıqları qiymətlərində Orta Kvadratik Xəta (MSE) ilə Orta Mütləq Xəta (MAE) funksiyalarının kombinə olunmuş formasıdır. Buna ehtiyac mənim intuisiyama görə belədir ki, biz modeli öyrədəcəyimiz məlumatların nə qədər səlis şəkildə müşahidə olunduğunu bilə bilmirik. Məsələn, bir İstilik Stansiyasındakı bir termometr sensorunun hesablayıcı cihaza göndərdiyi qiymətlər arasında 14 milyon selsi kimi bir müşahidənin olduğunu düşünün. Nəzərə alsaq ki, bu temperatur bizə ən yaxın Günəşin mərkəzində var, adi insan bunu görsə, adekvat reaksiya verər, müşahidə aparan cihazın xarab olduğunu dərhal başa düşərdi. Lakin model bu kənara çıxmanı (outlier) ciddiyə alacaqdır. Və bir adamın modelin öyrənəcəyi nümunələri tək-tək əllə yoxlayacaq halı olmadığından – ki, belə olsa, maşın öyrətməsi nəyə lazım – burada artıq məsələ bir nümunənin modelə nə qədər təsir etməsini təyin etməkdədir. Bayaq dediyimiz kimi dərhal anlaşılır ki, bir xəta funksiyasının qiymətinə bir müşahidəyə aid xəta ədədinin kvadratının əlavə edilməsi o ədədin sadəcə özünün daxil edilməsindən daha təsirli olacaqdır (xüsusən, ədəd çox böyük olduqda), deməli, modelə öyrədiləcək məlumat yığınına inanmırıqsa, burada xəta funksiyası kimi Orta Mütləq Xətanı (MAE) işlətməyimiz Orta Kvadratik Xətanı (MSE) işlətməyimizdən daha məqsədə uyğundur.
- Ancaq indi bir az fərqli ssenari düşünək. Təsəvvür edin, model əvvəlcədən öyrədilir, sonra istifadəyə buraxılır. Ancaq istifadə olunarkən yeni əlavə olunan məlumatlar əsasında da öyrənmə prosesi davam eləyir. Əgər üzdən də olsa, bizim ilkin öyrətməni apardığımız məlumatları gözdən keçirmə şansımız varsa, yaxşı olar ki, bizim özümüzün ilk başda daxil etdiyimiz məlumatın modelə təsirini çox, sonradan dinamik olaraq daxil olunacaq yeni məlumatların təsirini isə az eləyək. Və ya modelin hesabladığını cavabla real nəticənin fərqi (delta) ədədindən böyük olduqda verilənin kənaraçıxma (outlier) olduğu da hesab oluna bilər. Hansı ki, bu halda bu verilənin modelə təsirini azaltmaq üçün Orta Mütləq Xəta istifadə etmək daha yaxşıdır. Başqa sözlə, əgər risk daşıyırsa, modelə təsirini minimallaşdır. Yox, əgər inanırsansa, Orta Kvadratik Xəta-dan istifadə elə. Hansı ki, biz buna deyirik Huber. [4]
Düsturlar: [1]
Funksiya 6. LogCosh funskiyası
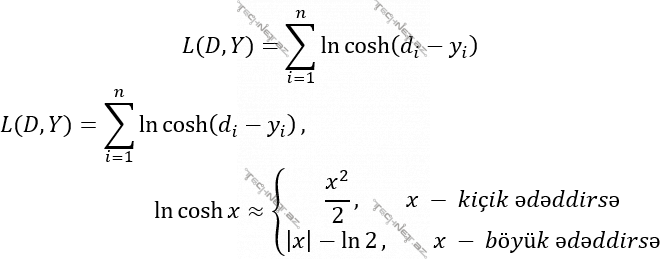
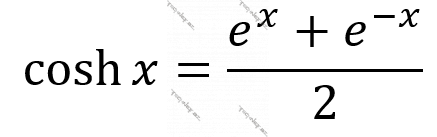
LogCosh funksiyası minimum nöqtəsi olmayan (əvəzində minimum aralığı olan) parabola kimidir və özünü iki fərqli funksiya kimi aparır. Yuxarıdakı ilk düsturdan da göründüyü kimi x kiçik ədəd olduqda model özünü MSE-yə, x böyük ədəd olduqda isə MAE-yə bənzədir. Bunu x-in kvadratı və mütləq qiyməti istifadə olunmasından görə bilərsiniz.
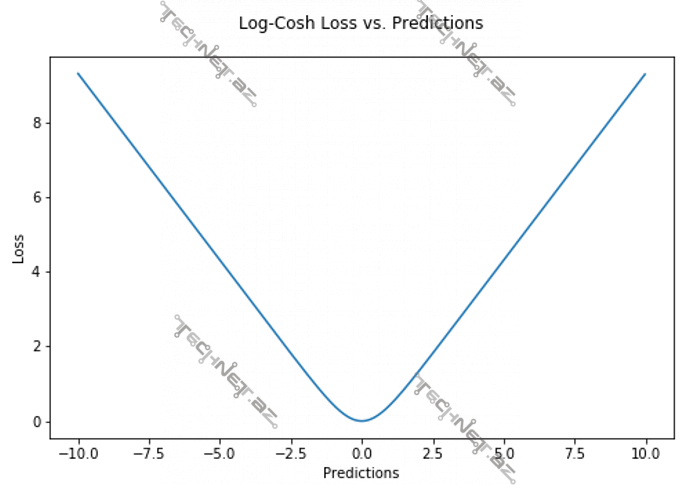
LogCosh funksiyasının istifadə olunma səbəbləri var:
- Belə ki, bu funksiyanın törəməsi bəsitcə tapıla bilən hiperbolik tangensdir (tanh). Bu isə funksiya optimallaşdırılarkən həmin funksiyanın asılı olduğu parametrlərə görə xüsusi törəmələrinin tapılmasını asanlaşdırır. [6] [7]
- Ancaq bir məsələ var ki, loqarifmə 0 vermək olmur. Praktikada bunun qarşısını almaq üçün xəta ədədinə çox kiçik (məs., 10^-13 kimi) bir ədəd əlavə olunur. Bu, hesablamalara çox təsir etmir, ancaq loqarifmin 0 olmasına da icazə vermir. [8]
Son bir qeyd: Huber və LogCosh funksiyalarını modelin öyrədiləcəyi/yoxlanacağı (train, validation data) məlumatlardan asılı olaraq performans (performans – burada modelin nəticələrini real öyrədilən qiymətlərə nə qədər yaxınlaşdırması) nöqteyi nəzərdən müqayisəli təhlil etmək faydalı ola bilər.
Funskiya 7. Puasson xətası (Poisson)
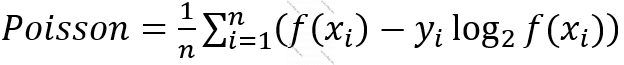
Modelin proqnozlaşdırdığı ədəd tam ədəd olmalı olduqda istifadə olunur. Başqa sözlə X verilənli müşahidələrin uyğun nəticələri puasson paylanmasıyla düzülübsə, bu xəta funksiyası istifadə olunur. Məsələn, verilmiş müddətdə verilmiş mobil şəbəkədə abunəliklərini dayandıran müştərilərin sayları əsasında müəssisənin faəliyyətinin təyin olunması kimi. Yəni müəyyən səbəblərə görə bu ay filan qədər istifadəçi abunəliklərini ləğv edib, indi təhlil etmək lazımdır ki, bu, nədən qaynaqlanıb və proqnozlaşdırmaq lazımdır ki, vəziyyəti bu cürə dəyişsək gələn ay nə qədər istifadəçi abunəliyini tərk edəcəkdir.
Entrofiya sistemdə qeyri-nizamlılığın nə qədər olduğudur. Amma bunun maşın öyrətməsi üçün mənası biraz başqadır. Məsələ burasındadır ki, klassifikasiya ilə məşğul olarkən biz ehtimal (müəyyən bir verilənin – X-in, hansısa sinfə məxsus olması ehtimalı) modelin aldığı ehtimal modelin nəticəsinin nə qədər qeyri-müəyyən olduğunu da göstərir. Bu “müəyyənlik əmsalı” öyrədilən təcrübələrin real ehtimal ədədlərinə nəzərən hesablanır.
Klassifikasiya məsələsini həll edən bir Süni Neyron Şəbəkəsinin son layında aktivasiya funksiyası kimi softmaks (softmax), siqmoid (sigmoid) istifadə olunduqda Xəta/İtki funksiyası kimi də Entrofiya-lardan biri istifadə olunur. [8] Bu ona görə belədir ki, softmaks və siqmoid aktivasiya funksiyaları 0-la 1 arasında ehtimal ədədi sayıla biləcək nəticələr verir.
Əgər hesablamalar aparılan ədədlər (y və f(x) qiymətləri) 0-la 1 arasındadırsa, Entrofiya istifadə olunur. Çünki bu halda model bu metodla Orta Kvadratik Xətada (MSE) olduğundan daha tez (fast) və vurdumduymaz (robust) (vurdumduymaz dedikdə – burada tək bir müşahidənin ümumi trendin müəyyən olunmasına çox ziyan verməməsi nəzərdə tutulur) öyrənir. [8]
Entrofiya ikili (binary), kateqorik (categoric), dağınıq (sparse categoric) olmaqla üç cür olur. Bunların üçünün də formulaları ortaqdır. Sadəcə ikilidə verilənlər iki sinifə ayrılır, kateqorikdə çox, dağınıq kateqorikdə isə kateoqorikdən entrofiya hesablanacaq ədədlərin ehtimal ədədi (0-la 1 arasında) yox, digər hər hansı şkalada ola bilməsi ilə fərqlənir. [10]
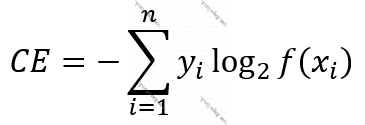
Funskiya 8. İkili Çarpaz Entrofiya (Binary Crossentrophy)
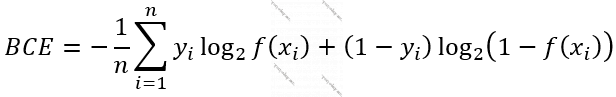
- Məsələ kimi verilən bir X-ı 2 sinifdən birinə ayırmaq qoyulubsa, məs., verilmiş şəkilin bir pişik və ya itin şəkli olduğunu müəyyən edəcək bir model quracağıqsa, yuxarıdakı düstur belə də (yuxarıdakı ilk düstur kimi) ifadə oluna bilər. [10]
- Adətən, Entrofiyalarda hesablamalar kiçik ədədlərlə getsin deyə alınan cəm n-ə bölünərək orta qiymət götürülür.
Funskiya 9. Kateqorik Çarpaz Entrofiya (Categorical Crossentrophy)
Funskiya 10. Dağınıq Kateqorik Çarpaz Entrofiya (Sparse Categorical Crossentrophy)
Funskiya 11. KL Fərqi (KL Divergence, Kullback-Leibler Divergence)
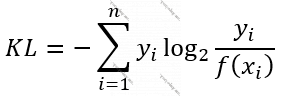
Bu metodda və entrofiyalarda 2 əsasdan loqarifm məlumatın kompüterdə nə qədər yer tutduğu, digər bir deyişlə məlumatdan nə qədər informasiya çıxarıla biləcəyi, yəni məlumatın informativliyi – məlumatın nə qədər informasiya daşıdığını ölçür. Nəzərə alın ki, yuxarıdakı düsturu belə də yazmaq olardı:
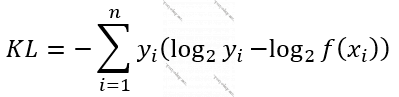
Düstur: [12], [13]
Bu da o deməkdir ki, biz real nəticələrdən ibarət ehtimal paylanması ilə modelin hesabladığı ehtimal paylanmasının informasiya tutumunu müqayisə edirik ki, real nəticədən qiymətlər approksimasiya olunarkən nə qədər informasiya itkisi baş verib onu müəyyən edək. İdeal halda real müşahidələr əsasında öyrədilmiş model nəticələr alarkən informasiya itkisi olmur. [12]
Mühüm ümumiləşdirmə:
[11]-də MSE, MAE, MAPE kimi Ən Kiçik Kvadratlar üsuluna (Least Squared Approach) aid metodların yalnız hansı halda mənalı olduğu izah olunur. Belə ki, bu üsulların ən bəsiti olan MSE modelin hesabladıqlarının real qiymətlərə bərabər olması ehtimallarının paylanmasının Normal Paylanma (Normal Distribution) olduğu halda Maksimal Doğruyaoxşarlıq Əmsalının (Maksimum Likelihood) maksimallaşdırılması MSE-nin minimallaşdırılmasıyla eyniləşir. Riyazi izahatı çox uzundur və [11]-də var, ancaq praktiki məsələ bundan ibarətdir ki, modelin nəticələrinin uyğun real nəticələrlə yaxınlığı normal paylanmadığı halda MSE, MAE, MAPE kimi üsullar absurdlaşır. Bu hallarda ya yuxarıda qeyd etdiyimiz, binary/categorical/sparce categorical kros-entrofiyalar, bəzən də KL Fərqi (KL Divergence, Kullback-Leibler Divergence) istifadə olunmalıdır.Son bir qeyd: KL Divergence və Crossentrophy də Huber və LogCosh-da olduğu kimi yaxşı olar ki, performans nöqteyi-nəzərdən data-ya (modelin öyrədiləcəyi/yoxlanacağı müşahidələrə (train, validation data)) uyğun olaraq müqayisəli təhlil edilsin.
Funksiya 12. Hinc xətası (Hinge)
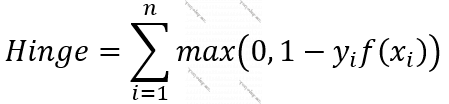
- Müşahidələr müəyyən bir sərhəd xəttinə olan məsafəsinə görə klassifikasiya olunur. Hinc xətasının klassifikasiya üçün istifadə olunan kross-entrofiyalardan fərqi odur ki, daha effektiv şəkildə işləyir, baxmayaraq ki, çox dəqiq olmaya da bilir.
- Hinc xətasında elə bir xətt (müşahidələr üç xüsusiyyətlə təyin olunursa bu, bir müstəvi olacaq və s.) təyin olunmağı hədəflənir ki, müşahidələr bu xəttə maksimal uzaq olsun və bu xəttin bir tərəfində qalanlar mənfi, digərləri müsbət olsun. Yəni Hinc xətasının işlətdiyi (yi, f(xi)) cütləri ədədlərin işarəsini göstərən -1-lə 1 arasında ədədlərdən ibarət olacaq. Bu isə o deməkdir ki, məsələn, üç sinifə bölünmə üçün yif(xi) qiymətlərinin [10, 8, 8] olması ilə [10, -10, -10] olması arasında fərq yoxdur. Hinc xətası müşahidəyə (+, -) işarə verdikdən sonra optimallaşdırmanı davam etdirməyə ehtiyac duymur. Ancaq eyni nümunə kross-entrofiyanın qarşısına çıxsaydı optimallaşdırma davam edərdi. Buna görə, Hinc sürətli cavab versə də dəqiq hesabladığından əmin ola bilmədiyimiz, klassifikasiya üçün istifadə olunan xəta/itki funskiyasıdır.. [14] [15]
- Real zamanlı öyrətmə işlərində daha çox istifadə olunur. Sürətli ola bilməsinə görə.
Funksiya 13. Kvadratik Hinc (Squared Hinge)
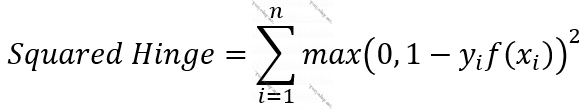
- Hinc-i hamarlaşdırır. Bu isə optimallaşdırmada ədədi üsullarla işləməyi asanlaşdırır. [15] Kerasla model qurarkən, optimizor-a sgd, adam və s. kimi arqumentlər verə bilirik. Bu optimizor-lar bir-birindən fərqli olsalar da əksəriyyəti bir-birilə oxşar yolları izləyir. Adətən, funksiyanın törəməsinə ehtiyac duyulur və funksiyanın hamar olması törəməsinin tapıla biləcəyini şərtləndirir.
Son bir qeyd: Hinge və Squared Hinge-i fərqli optimizor-larla performans cəhətdən verilmiş data-ya uyğun müqayisə etmək yaxşı olardı.
Funksiya 14. Kateqorik Hinc (Categorical Hinge)
- “Funksiya 12″dəki düstur burada da istifadə olunur. Hətta Hinge (12) Kateqorik Hinc-in xüsusi halı sayıla bilər. Bir halda ki, Hinc və Kvadratik Hinc yəni müşahidələr iki sinfə klassifikasiya olunduqda istifadə olunan keras obyektidir, Kateqorik Hinc ikidən çox sinfə klassifikasiya apararkən istifadə olunur. [16]
Funskiya 15. Kosinus yaxınlığı (Cosine Similarity) [17]
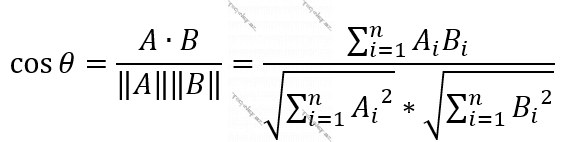
Tutalım ki, şəklinə baxaraq gülləri bir-birindən seçən bir model hazırlayırıq. Təsəvvür edin modeli öyrədərkən sırayla məlumatlar əsasında ayrılacaq sinifləri {qərənfil, çobanyastığı, roza} deyə düşünmüşük. Məsələn, öyrətmək üçün modelə ötürdüyümüz şəkil çobanyastığıdırsa, nəticəni y = [0, 1, 0] olaraq daxil edəcəyik. İndi təsəvvür eləyin, modeli öyrətdiyimiz o şəkli modeli öyrətdikdən sonra modelə verib [0.08, 0.91, 0.01] kimi bir nəticə almışıq. Burada vektoru təşkil edən hər element bir sinfi təmsil edir və bu iki vektorun – real nəticə və modelin hesablayacağı, arasındakı bucağın kosinusundan istifadə edərək bu vektorların bir-birinə nə qədər yaxın-uzaq olduğunu deyə bilərik. Kosinus hər (0 + 2πk, k = 1, 2, …) dərəcədə, yəni iki vektor üst-üstə düşəndə 1 alır deyə iki vektor arasındakı bucağın kosinusu 1 olduqda deyirik ki, bu iki vektor – real nəticə ilə proqnozlaşdırılan, eyni vektorlardır, yəni vəziyyət əladır. İki vektor arasındakı bucağın kosinusu -1 aldıqda iki vektor bir-birinin əksinədir, yəni modelin aldığıyla reallıqda müşahidə olunanın bir-birinə dəxli yoxdur.
Bu xəta funksiyası iki vektor arasındakı bucaqdan istifadə etməkdən daha yaxşı yol olmadıqda istifadə olunur. Məsələn, təsəvvür edin, imtahan cavablarına baxaraq hansı tələbələrin bir-birindən köçürdüyünü müəyyən etməyə çalışırıq. Bu halda məlumatların qruplaşdırılacaqları konkret sinif sayını bilmirik. Olsun ki, Mahmudla Arif bir-birindən, Asif, Vasif, Ağasiz ayrı-ayrılıqda bir-birilərindən, Nazimlə Kazım da bir-birilərindən köçürüblər. Və ya olsun ki, elə hala rast gələcəyik ki, orada hamı eyni şeyi köçürüb və ya heç kim köçürməyib. Heç olmasa cəhənnəm bilsəydik ki, qrupda köçürənlər hamısı eyni mənbədən köçürüblər, onda köçürənlər və köçürməyənlər kimi iki qrup təyin edər, işi həll eləyərdik. Ancaq bizim məsələmizdə daha yaxşısı belə olardı ki, hər tələbənin cavabını müəyyən bir vektor kimi düşünək (məsələn, maksimal söz sayı kimi 500 götürüb, hər nömrədə tələbənin yazdığı söz olmaqla təşkil olunmuş bir sözlər siyahısı kimi bir vektor), sonra bu vektorların hər biri ilə digərləri arasındakı bucağının kosinuslarını hesablayaraq bu vektorların hər birinin hansına daha yaxın olduğunu belə müəyyən eləyək. Və əgər iki vektorun bir-birinə yaxınlığı marjinal deyəcək qədər qeyri-adidirsə, bu adamları köçürmüş sayaq (və ya bundan şübhələnək).
Mühüm qeydlər
- İkili, Kateqorik və Dağınıq Kateqorik kross-entrofiya xəta funksiyalarından biri istifadə olunduqda Süni Neyron Şəbəkəsinin son layında/səviyyəsində (son layer-də) siqmoid və ya softmaks aktivasiya funksiyası istifadə olunur, çünki bu aktivasiya funksiyaları 0-la 1 arasında qiymətlər alır.
- Düsturlarını verdiyimiz bütün funksiyalar itki (loss) yox, xəta (cost) funksiyalarıdır. Bu iki anlayış arasındakı fərq bundan ibarətdir ki, itki –“loss” funksiyası bir müşahidənin xəta ədədini tapır, xəta – “cost” funksiyası isə bütün müşahidələrin itki – “loss” funksiya qiymətləri cəmidir. Başqa sözlə, yazdığımız funksiyalardan cəm (∑) işarələrini silərsək, itki – “loss” funksiyalarını alacağıq. [8]
- Kosinus yaxınlığı funksiyasını çıxmaqla digər xəta funksiyalarını iki sinfə bölmək olar: Reqressiya və Klassifikasiya.
- Reqressiya verilmiş sayda xüsusiyyət əsasında müşahidələrdən bir real və ya tam ədəd tapılmasıdır. Yəni X vektoruna uyğun f(X) cəmisi bir ədəddir.
- Klassifikasiyada isə adətən müşahidələrin klassifikasiya olunacağı siniflərin hər biri üçün bir ədəd tapılır, bu ədədlərdən maksimal olanı götürülür. Məsələn, boy və kütləni müşahidələrin xüsusiyyətləri götürsək və bu müşahidələr əsasında bu xüsusiyyətlərə sahib canlının pişik, it, yoxsa doşan olduğunu tapmağa çalışsaq aşağıdakı kimi bir forma işlədilə bilir.
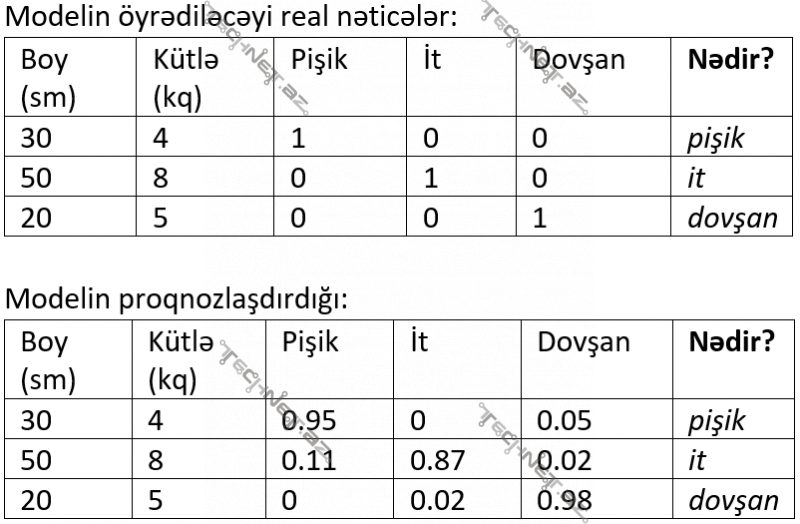
Xəta/itki funksiyalarının sinifləşdirilməsi:
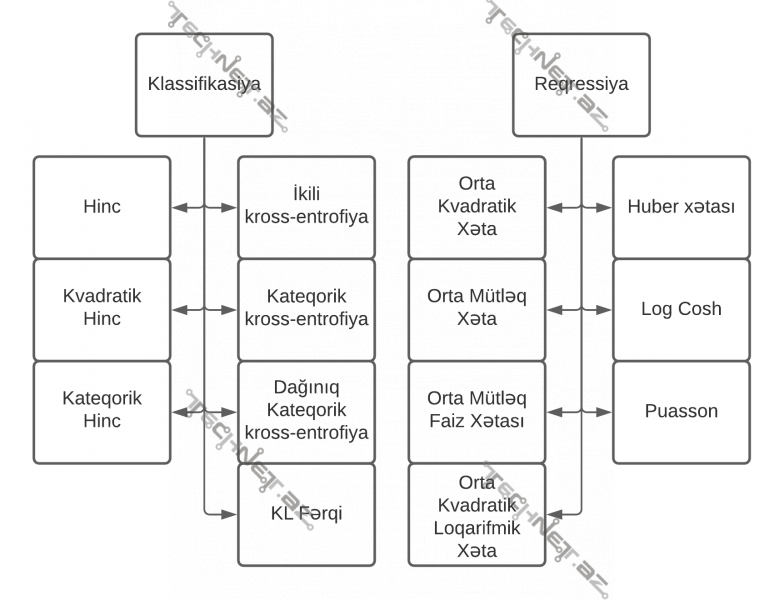
Xəta funksiyası seçimi edərkən atılmalı addımlar ardıcıllığı
- Qurulacaq modelin Klassifikasiya, Reqressiya, yoxsa başqa bir məsələni həll etdiyinin təyini.
- Məsələnin təyinatına uyğun olaraq Klassifikasiya və ya Reqressiya-da istifadə olunan xəta funksiyalardan bir neçəsinin seçilməsi.
- Modelin nə qədər tez öyrədilməli olduğu ilə müşahidələrin modelə nə qədər çox öyrədilməsi – modelin dəqiqliyi arasında hansının daha mühüm olduğunun seçilməsi.
- Prioritetin öyrədilmə sürəti və ya öyrədilmə dərəcəsi olması əsasında məsələnin təyinatına uyğun xəta funksiyalarının seçilməsi.
- Seçilmiş xəta funksiyalarına uyğun gələcək Süni Neyron Şəbəkəsinin son layında/səviyyəsində (layer-ində) aktivasiya funksiyalarından hansıların istifadə oluna biləcəyinin təyini və bu aktivasiya funksiyalarından birinin/bir neçəsinin seçilməsi.
- Seçilmiş parametrlərə uyğun olaraq modelin öyrədilməsinə cəhdlər edib bu cəhdlərin nəticələrinin müqayisə edilməsi.
- Yekunda istifadə olunacaq xəta funksiyasının qərarlaşdırılması.
Nəticə
Tensorflow platformasında keras kitabxanasından istifadə edərək asan və tutarlı yolla Süni Neyron Şəbəkəsi qurmaq olur. İstənilən optimallaşdırmaya ehtiyac duyan model kimi Süni Neyron Şəbəkəsinin də ən mühüm ünsürlərindən biri istifadə etdiyi xəta funksiyasıdır (cost function). Biz bu məqalədə keras kitabxanasında istifadə oluna bilən xəta funksiyalarının izahatlarını və istifadə məqamlarını mümkün qədər əhatə etməyə çalışdıq. Fəqət şübhəsiz ki, verilmiş tapşırıq üçün hansı xəta funksiyasının istifadə olunacağı o tapşırığın təyinatından və yerinə yetiriləcəyi mühitdən asılıdır. Ona görə də, əgər bu funksiyalardan sadəcə biri bütün hallara uyğun gəlsəydi bu qədər işlək funksiya olmazdı qənaətimizə arxalanaraq məqaləmizi burada bitiririk. Keras kitabxanasının köməyi ilə Süni Neyron Şəbəkə qurarkən istifadə edə biləcəyimiz funksiyaların inglis dilində adı və istifadəsinə dair detallara buradan (https://www.tensorflow.org/api_docs/python/tf/keras/losses) nəzər sala bilərsiniz.
Ədəbiyyat
[1] https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0 [2] https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2015-107.pdf [3] https://peltarion.com/knowledge-center/documentation/modeling-view/build-an-ai-model/loss-functions/mean-squared-logarithmic-error-(msle) [4] https://medium.com/@gobiviswaml/huber-error-loss-functions-3f2ac015cd45 [5] http://www.mathcentre.ac.uk/resources/workbooks/mathcentre/hyperbolicfunctions.pdf[6] https://openreview.net/forum?id=rkglvsC9Ym
[7] https://www.youtube.com/watch?v=q-iV83HIvP0 [8] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/ [9] https://peltarion.com/knowledge-center/documentation/modeling-view/build-an-ai-model/loss-functions/poisson [10] https://towardsdatascience.com/cross-entropy-loss-function-f38c4ec8643e [11] https://scholarworks.utep.edu/cgi/viewcontent.cgi?article=2188&context=cs_techrep [12] https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained [13] https://machinelearningmastery.com/divergence-between-probability-distributions/ [14] https://rohanvarma.me/Loss-Functions/#:~:text=The%20main%20difference%20between%20the,from%20a%20maximum%20likelihood%20estimate [15] https://machinelearningmastery.com/how-to-choose-loss-functions-when-training-deep-learning-neural-networks/ [16] https://www.machinecurve.com/index.php/2019/10/17/how-to-use-categorical-multiclass-hinge-with-keras/#:~:text=The%20name%20categorical%20hinge%20loss,already%20implies%20what’s%20happening%20here%3A&text=That%20is%2C%20if%20we%20have,%2C%200%2C%201%5D). [17] https://towardsdatascience.com/a-guide-to-neural-network-loss-functions-with-applications-in-keras-3a3baa9f71c5 [18] https://medium.com/analytics-vidhya/a-comprehensive-guide-to-loss-functions-part-1-regression-ff8b847675d6


