Çoxluqlar üzərində əməllər 3-cü hissə (RİGHT OUTER JOİN)

Salam Dostlar.

Bu gün mövzunun davamı olaraq çoxluqlar üzərində əməllər və onların verilənlər bazasında istifadəsi barədə bəhs olunacaq. Məqalənin ikinci hissəsində verilənlər bazasında olan cədvəllər arasında münasibətlər qurduq, iki çoxluğun fərqi əməliyyatını etdik və LEFT OUTER JOİN əməliyyatı ilə tanış olduq. Ümumilikdə, çoxluqlar üzərində mövcud olan üç əsas əməllər bizim maraq dairəmizdədir: çoxluqların kəsişməsi, çoxluqların fərqi və çoxluqların birləşməsi. Bu gün çoxluqların fərqi mövzusunu davam edəcəyik.

Bildiyimiz kimi, SQL adətən elementləri cədvəl sətirlərindən ibarət olan mürəkkəb çoxluqlarla işləyir. İki çoxluq arasında münasibət yaradılanda bu çoxluqların elementlərinin atributları müqayisə edilir. Başqa sözlə desək, cədvəlin sətirlərini izah edən sütunlar müqayisə edilir. Riyaziyyatın çoxluqlar nəzəriyyəsini verilənlər bazasında istifadə etmək üçün bir daha təkrar etməliyik: bazada ayrı-ayrı cədvəllər (daha doğrusu münasibətlər) – çoxluqlar, cədvəllərin sətirləri çoxluğun elementləri və cədvəlin sütunları elementlərin atributları adlandırılır. Keçən dərslərimizdən bizə tanış olan təsvirimizə bir daha baxaq:

Həmin bazada olan cədvəllərin hər biri ilə ayrı-ayrılıqda işləmək olar; məsələn: “Personal” cədvəlindən əməkdaşın ünvanları, adı, soyadı barədə məlumat əldə etmək olar. Lakin elə məlumatlar var ki, iki və ya bir neçə cədvəldən alınır. Məsələn: əməkdaşın çalışdığı departament barədə məlumatı əldə etmək üçün “Personal” və “Department” cədvəlləri arasında münasibət yaratmalıyıq. Həmin cədvəlləri çoxluqlar şəklində təsvir etsək riyaziyyatda olan çoxluqların birləşməsi, kəsişməsi və fərqi əməliyyatlarını həyata keçirə bilərik.

Çoxluqların fərqi əməli barədə keçən dərsimizdə danışdıq. A çoxluğunun B-dən fərqini tapdıq. İki çoxluq arasında fərq varsa, deməli ikinci çoxluq da birincidən fərqlənir, yəni B çoxluğu da A-dan fərqlənir. Çoxluqların fərqi tərifinə bir daha baxaq:

Tərif. A və B çoxluqlarının fərqi A çoxluğunun B-yə daxil olmayan elementləri çoxluğuna deyilir və A \ B kimi işarə olunur. Başqa sözlə, B çoxluğuna daxil olmayan A çoxluğunun bütün elementlərindən ibarət olan çoxluğa A və B çoxluqlarının fərqi deyilir.

Bunun əksini, yəni B-nin A-dan fərqini isə belə tərif etmək olar:

B və A çoxluqlarının fərqi B çoxluğunun A-ya daxil olmayan elementləri çoxluğuna deyilir və B \ A kimi işarə olunur. Başqa sözlə, A çoxluğuna daxil olmayan B çoxluğunun bütün elementlərindən ibarət olan çoxluğa B və A çoxluqlarının fərqi deyilir.

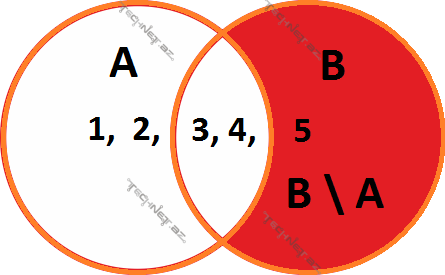
Çoxluqların fərqini rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5 rəqəmlərindən ibarətdir. Bu iki çoxluğun fərqi B çoxluğuna daxil olan 5 rəqəmindən ibarət yeni çoxluq olacaq, çünki 3 və 4 rəqəmləri A çoxluğunda da var, 5 rəqəmi isə A-ya daxil deyildir.

Əgər А={1,2,3,4}, B={3,4,5}, onda B \ A = {5}

Yuxarıdakı “Əməkdaşlar” bazasında olan “Personal” mürəkkəb çoxluğunu aşağıdakı şəkildə təsvir edə bilərik:

Fərz edək ki, a, b, c, d, e – “Per_İD, FirstName, LastName, Address, Dep_İD” atributlarıdır  və A çoxluğu həmin atributları olan elementlərdən ibarətdir:

A = {a, b, c, d, e}

 “Department” çoxluğunu aşağıdakı şəkildə təsvir edə bilərik:

Fərz edək ki, e, f – “Dep_İD, Department” atributlarıdır və B çoxluğu həmin atributları olan elementlərdən ibarətdir:

B= {e, f}

Sorğu formalaşdıraq: Heç bir əməkdaşın çalışmadığı departamentləri tapın. İkinci variant: heç bir işçisi olmayan departamentləri tapın.

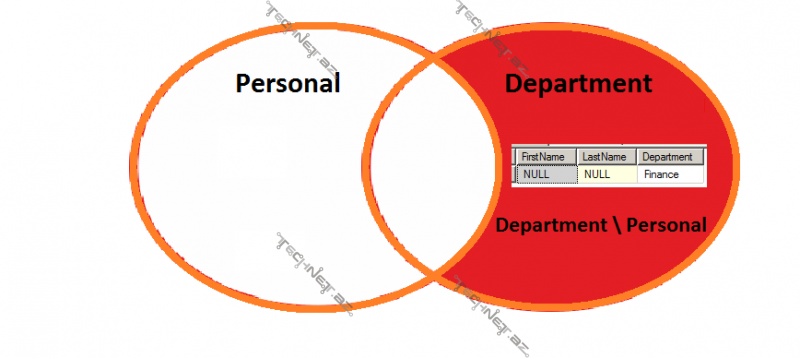
Sorğunu çoxluqlar nəzəriyyəsinə uyğun dəqiqləşdirək: cavabı cəmi bir cədvəldən: “Personal” cədvəlindən ala bilmərik, çünki şirkətin departamentləri barədə məlumat başqa cədvəldə yerləşir. Deməli, sorğu belə olacaq: “Department” çoxluğuna daxil olan və eyni zamanda “Personal” çoxluğuna daxil olmayan məlumatı tapın, yəni elə bir məlumatı ki, “Department” cədvəlində olsun, “Personal” cədvəlində isə olmasın. Başqa sözlə, biz “Department”  və “Personal” çoxluqlarının fərqi əməliyyatını etməliyik.

Bu iki çoxluğun fərqi bizə nə verir. Gəlin, ilk öncə həllini tapaq:

B \ A = {f}

Deməli, “Department” çoxluğuna daxil olan və eyni zamanda “Personal” çoxluğuna daxil olmayan bir atributu (sütunu) olan element vardır. Dep_İD atributu isə həm “Personal” və həm də “Department” çoxluğuna daxildir. Yuxarıda qeyd etdik ki, atributlar mürəkkəb çoxluğun elementlərini izah edən parametrlərdir, verilənlər bazası terminlərində isə cədvəlin sütunlarıdır. Deməli, biz bir cədvələ daxil olan və digər cədvələ daxil olmayan atributları (sütunları) olan bütün sətirlərdən ibarət yeni bir cədvəl əldə etdik.

Daha aydın olması üçün yaratdığımız cədvəllər üzərində göstərək:

Fərz edək ki, bazamız üç cədvəldən ibarətdir: “Personal”, “Departament” və “Phone”

“Personal” cədvəli:

“Dapartment” cədvəli

“Phone” cədvəli

Qoyulmuş sualın cavabını tapmaq üçün biz iki cədvəllə işləməliyik – “Personal” və “Department” cədvəlləriylə. Gördüyümüz kimi, hər iki cədvəldə eyni sütun var – “Dep_İD” sütunu. Bu sütun həm “Department”, həm də “Personal” çoxluğundakı elementlərin bir atributudur. “Department” çoxluğunda cəmi beş elementimiz var və hər birinin “Dep_İD” atributu vardir. Yalnız “Finance” elementinin “Dep_İD” atributu “Personal” çoxluğundakı “Dep_İD” atributu ilə üst-üstə gəlmir. “Department” çoxluğunun bütün digər elementləri “Personal” elementləri ilə eyni bir atributu (Dep_İD) olduğu üçün çoxluqlar nəzəriyyəsinə əsasən həmin elementlər hər iki çoxluğa daxildir. Çoxluqlar nəzəriyyəsinə əsasən çoxluğun elementi sadə rəqəmdən və ya başqa sadə qiymətdən daha böyükdürsə, çoxluğun hər elementinin xüsusiyyətlərinin təsvir edən  bir neçə atributu (və ya verilən bitləri) vardır. İki çoxluq arasında münasibət yaradılanda bu çoxluqların elementlərinin atributları müqayisə edilir və atributlardan heç olmasa biri hər iki çoxluqda eynidirsə  həmin elementlər həmin çoxluğa daxil olunmuş qəbul olunur.

Yuxarıda dedik ki, biz bir çoxluğa (cədvələ) daxil olan və digər çoxluğa (cədvələ) daxil olmayan atributları (sütunları) olan bütün elementlərdən (sətirlərdən) ibarət olan yeni bir çoxluq (cədvəl) əldə etdik.

Beləliklə, “Department” və “Personal” çoxluqlarının fərqi nəticəsində yeni bir çoxluq alırıq:

Lakin sualımıza diqqət yetirsək görərik ki, bizdən tələb olunan yalnız departamentlərin və orada çalışan əməkdaşların adlarıdır, yəni cədvəllərdə olan ünvan və digər parametrlər tələb olunmur. Sorğu belə idi: Heç bir əməkdaşın çalışmadığı departamentləri tapın. Yəni departamentin adını və orada heç bir əməkdaşın çalışmadığı barədə məlumatı ekranda göstərin.  Nəticədə alırıq:

Nəticəmizdə cəmi bir sətir və ya element var: “Finance” departamenti. Bəs digər elementlər necə oldu? Səbəbi isə çox sadədir: heç bir əməkdaşın çalışmadığı, yəni heç bir işçisi olmayan cəmi bir departamentimiz var- Finance departementi. Çoxluqlar terminlərində isə: “Department” çoxluğunun ”Finance” elementinin “Dep_İD” atributu “Personal” çoxluğundakı “Dep_İD” atributundan fərqlidir və buna görə də həmin element “Personal” çoxluğuna daxil deyildir və yalnız “Department” çoxluğuna daxildir. Yuxarıda qeyd etdik ki, iki çoxluq arasında münasibət yaradılanda bu çoxluqların elementlərinin atributları müqayisə edilir. Tərifə birdə qayıdaq: A çoxluğuna daxil olmayan  B çoxluğunun bütün elementlərindən ibarət olan çoxluğa B və A çoxluqlarının fərqi deyilir. “Personal” çoxluğuna daxil olmayan “Department” çoxluğunun bütün elementlərindən ibarət olan çoxluğunda cəmi bir elementimiz var – “Finance”:

Əslində biz məqaləmizin bu hissəsində verilənlər bazasının sorğu dilinin (SQL) daha bir əməliyyatı (daha doğrusu sorğusu) ilə tanış olduq. Bu əməliyyat SQL – də JOİN adlandırılır. Bizim etdiyimiz əməliyyat isə OUTER JOİN adlandırlır. Sualımızı SQL dilinə çevirək: departamentlərin adlarını və orada heç bir əməkdaşın çalışmadığı barədə (adı, soyadı) məlumatı “Personal” və “Department” cədvəllərindən alın. Sorğunun “heç bir əməkdaşın çalışmadığı” hissəsi xüsusi maraq doğurur. Yəni bizə bütün departamentlər lazım deyil, yalnız heç bir əməkdaşın çalışmadığı departamentlər lazımdır. Başqa sözlə “Personal” cədvəlinə aidiyyəti olmayan departamentləri tapın. Həmin şərtə əsasən yalnız “Personal” cədvəlində “Finance” departamentinin “Dep_İD” atributu NULL qiyməti alıb, yəni “Personal” cədvəlində heç bir qiyməti yoxdur.

İngilis dilinə çevirsək:

SELECT FirstName, LastName, Department

FROM Personal

RIGHT OUTER JOIN Department ON Personal.Dep_ID = Department.Dep_ID

WHERE Personal.Dep_ID IS NULL

SQL dilinin operatorları və sintaksisi barədə ətraflı məlumat növbəti məqalələrdə veriləcək. Burada biz verilənlər bazasında cədvəllərin arasında münasibətlərin yaradılması prosesini nümayiş etmək və verilənlərin münasibətli modelini izah etmək üçün SQL operatorlarından istifadə etdik. Yuxarıdakı nümunəmizdə biz OUTER JOİN əməliyyatının bir növü olan RİGHT OUTER JOİN əməliyyatı ilə tanış olduq. Lakin yuxarıda göstərdiyimiz nümunədə şərt vardır: “Personal” cədvəlində “Dep_İD” atributu olmayan (NULL olan) sətirlər “Department” cədvəlindən seçilməlidir. Həmin şərt SQL dilində WHERE A.Key İS NULL operatoru ilə yazılır və “Right Excluding JOIN” (Sağ istisna birləşməsi) adlandırılır. Həmin əməliyyat çoxluqlar nəzəriyyəsində olan çoxluqların fərqi əməli ilə eynidir.

 İstisnasız (adi) RİGHT OUTER JOİN əməliyyatı göstərmək üçün yeni sorğu formalaşdıraq:

Bütün departamentlərin və orada çalışan əməkdaşların siyahısını verin.

Sorğunu çoxluqlar nəzəriyyəsinə uyğun dəqiqləşdirək: cavabı cəmi bir cədvəldən: “Department” cədvəlindən ala bilmərik, çünki şirkətin əməkdaşları barədə məlumat başqa cədvəldə yerləşir. Deməli, sorğu belə olacaq: “Department” çoxluğuna daxil olan və “Personal” cədvəlinə uyğun olan bütün məlumatı tapın, yəni elə bir məlumatı ki, “Department” cədvəlində tam şəkildə olsun, eyni zamanda “Personal” cədvəlinə də uyğun gəlsin.

Verilmiş sorğunun izahını rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5 rəqəmlərindən ibarətdir. 3 və 4 rəqəmləri həm A, həm də B çoxluğuna daxildir. Deməli, B çoxluğuna daxil olan bütün rəqəmlərin və A çoxluğunda daxil olan B çoxluğuna uyğun olan rəqəmlərin çoxluğu 3, 4 və 5 rəqəmlərindən ibarət çoxluqdur:

Verilmiş sorğunun cavabını cədvəllərimiz üzərindən tapmaq üçün biz iki cədvəllə işləməliyik – “Personal” və “Department” cədvəlləriylə. Gördüyümüz kimi, hər iki cədvəldə eyni sütun var – “Dep_İD” sütunu. Lakin “Department” cədvəlində olan bir “Dep_İD”  sütunu “Personal” cədvəlindəki “Dep_İD” sütununda olan qiymətlərdən fərqlidir, bütün digər qiymətlər isə eynidir.

Yuxarıda dedik ki, “Department” çoxluğuna (cədvəlinə) daxil olan bütün elementlərindən və “Personal” çoxluğuna daxil olan “Department” çoxluğuna uyğun olan elementlərin çoxluğu bizim sorğunun nəticəsi olacaq:

Beləliklə, yeni bir çoxluq alırıq:

Lakin sualımıza diqqət yetirsək görərik ki, bizdən tələb olunan yalnız departamentlərin və orada çalışan əməkdaşların adlarıdır, yəni cədvəllərdə olan ünvan və digər parametrlər tələb olunmur. Sorğu belə idi: Bütün departamentlərin və orada çalışan əməkdaşların siyahısını verin. Yəni bütün departamentlərin adını, orada çalışan əməkdaşların adını və soyadını ekranda göstərin.  Nəticədə alırıq:

Nəticəmizdə altı sətir və ya element var. Finance departamentinin qarşısında NULL qiyməti var və görmədiyimiz bir element – Tale Abbasov adında əməkdaşdır. Səbəbi isə çox sadədir: Finance departamentində heç bir əməkdaş çalışmır və Tale Abbasov heç bir departamentdə çalışmır.

Məqalənin bu hissəsində verilənlər bazasının sorğu dilinin (SQL) daha bir əməliyyatı (daha doğrusu sorğusu) ilə tanış olduq. Bu əməliyyat SQL – də JOİN adlandırılır. Bizim etdiyimiz əməliyyat isə RİGHT OUTER JOİN adlandırlır. Sualımızı SQL dilinə çevirək: bütün departamentlərin adı, orada çalışan əməkdaşların adı və soyadı barədə məlumatı “Personal” və “Department” cədvəllərindən alın. İngilis dilinə çevirsək:

SELECT FirstName, LastName, Department

FROM Personal

RIGHT OUTER JOIN Department ON Personal.Dep_ID = Department.Dep_ID

SQL dilinin operatorları barədə ətraflı məlumat növbəti məqalələrdə veriləcək. Burada biz verilənlər bazasında cədvəllərin arasında münasibətlərin yaradılması prosesini nümayiş etmək və verilənlərin münasibətli modelini izah etmək üçün SQL operatorlarından istifadə etdik. Yuxarıdakı nümunəmizdə biz RİGHT OUTER JOİN əməliyyatı ilə tanış olduq. Ümumiyyətlə, qeyd etmək lazımdır ki, OUTER JOİN əməliyyatının üç növü vardır: LEFT OUTER JOİN, RİGHT OUTER JOİN və FULL OUTER JOİN.

Məqaləmizin üçüncü hissəsinin sonuna gəlib çatdıq. Bu hissədə riyaziyyatın çoxluqlar nəzəriyyəsində olan çoxluqların fərqi, verilənlər bazasında ayrı-ayrı cədvəllər arasında münasibətlərin yaradılması və RİGHT OUTER JOİN əməliyyatı barədə bəhs etdik.

Ümid edirəm ki, faydalı olacaq.

Məqalənin növbəti hissəsində çoxluqların birləşməsi və SQL dilinin FULL OUTER JOİN əməliyyatı barədə ətraflı məlumat verməyə çalışacağam.

Məqalənin əvvəlki hissələrini aşağıdakı keçidlərdən tapa bilərsiniz:

Çoxluqlar üzərində əməllər 1-ci hissə (İNNER JOİN)

Çoxluqlar üzərində əməllər 2-ci hissə (LEFT OUTER JOİN)